FPGA Mandelbrot Set Computation
After learning how to display VGA graphics from a FPGA board, from a course project, I wanted to go further. I was fascinated by the concept of running computation directly on hardware, with no operating system. I had come to realize that in hardware, "parallelization" is literal -- you can literally synthesize another unit of computation and place it in parallel!
Drawing fractals is a classic highly-parallelizable-problem, so: in my spare time I wrote Verilog code, from scratch, to compute and display the Mandelbrot set fractal on FPGA hardware.
(from a blog post I wrote in 2009, halfhourhacks 2009-05-10-fpga-mandelbrot-set-computation.html)
In April, I worked on an interesting project outside of class. I wrote Verilog code to compute and display the Mandlebrot set fractal on FPGA hardware. Besides the tool-generated multipliers, memory banks, and vga output, I wrote all of the logic from scratch.
My motivation was essentially to experience high-speed mathematical operations, creating pure computation with no operating system or even CPU. I chose to draw the Mandelbrot set knowing that it was a highly parallelizable problem; I was fascinated by how when running on physical hardware like this there is *physical* parallelization as data moves through each gate.
The FPGA, or field-programmable gate array, essentially consists of a large number of logic gates that can be configured to perform computation. Developing for this platform feels foreign at first. There is no CPU, and consequently, there isn't an inherent execution step going from one instruction to the next. One needs to set up registers and state machines to determine which chains of logic gates the data will flow through. Ideally you can use the fabric spatially, setting up associations and connections between components and placing logic in parallel. Making use of parallelism can lead to excellent performance solving certain problems.
The FPGA device once loaded can only perform one task. A CPU, like the processor on the computer you are currently using, is general purpose, and reads from a list of instructions to perform. If given a new list of instructions, it is able to execute them. The 'program' I describe here, on the other hand, has no such list of instructions, it is physically only capable of this one task.
I still use a clock signal, though, in common with a PC, but during each tick of the clock, several multiplications and additions and memory reads are done at the same time -- very different than what occurs in a CPU. It is an interesting trade-off at this level that resource-expensive mdoules like multipliers will limit the maximum clock speed.
The Mandelbrot image is a cliché, but it is a parallelizable problem and has interesting opportunities for optimization. I used four components to solve the problem. A "Child" unit receives x,y coordinates and screen coordinates as input. It has an internal state machine. In `State_calc it performs one iteration of the Mandelbrot set computation. If the current value is too great (pixel is not in Mandelbrot set), or the number of iterations is sufficiently large (pixel is probably in Mandelbrot set), the state moves to `State_write which will write the result to memory by setting a write-enable flag. `State_acqnew retrieves the next value that should be computed and resets computation. Each "child" had a separate RAM unit so that it could independentally read and write to memory.
The 'Parent' unit contains several Child units and is responsible for dividing work among them. The current set of uncomputed values is given to the first child that is not busy.
The ColorMap unit maps the number of iterations to an R,G,B color, using some shifting to unpack colors from distributed ROM. Because this isn't an art project, I just looked up a shareware program called UltraFractal and recreated its default color pallette.
The VGA unit reads a value from memory, translates it to a color with the ColorMap unit, and sets output voltage on a physical pin. VGA scans through the image more quickly than values can be computed, and so I needed a buffer of separate memory.
I could then connect these units. The design was intentionally flexible with regard to the number of Child units. This number can be increased until reaching the capacity of the fabric, so that my design will easily scale if a FPGA with more gates is available.
Simulation
I wrote a C implementation of the Child algorithm. Because this prototype ran quickly, I could use it to experiment with the color table, number of iterations, and initial view.
I made a Verilog module called vga_simulator that could be used in ModelSim. This module received r, g, and b values with the same interface as an actual vga output. It wrote to a file on disk that could later be transcribed into a standard bitmap image.
I translated my design to Verilog, using the vga_simulator to test results. I used fixed point arithmetic, which was sufficient for the problem; floating point would not have been practical for the scope of my project. It was fun to avoid multplication as many places as possible, particularly to make multiplies by a constant into shifts and adds. I started with just one Child unit, drawing to black and white, to reduce possible points of error, before slowly re-adding functionality.
One obstacle was that I needed to use both signed reg and signed shift (>>>) in a certain part of my arithmetic. Coming from C, I had not realized that I needed separate syntax for signed shift, and so it took some time to realize why the results were incorrect.

(This picture shows the result of a bug in my scheduler. Sometimes it is broken code that makes the best-looking results.)
With a working simulation, and a highly-visible counter that showed how many clock ticks were necessary to complete computation, I could work on optimization.
Optimization
Optimizing for this platform was a different experience than optimizing typical software. As well as taking less clock ticks to complete, the program also has to be optimized in space, to reduce the number of gates needed. This led to behavior that I did not expect: In typical software optimization, I will often check for conditions so that I can do less work if necessary, and skip going down an unneeded code path. In hardware, though, conditions are space-expensive, because each requires wiring. "Skipping a code path" is sometimes meaningless - the entire path is done in one clock tick anyways, and it is taking up space, so it is often better to always perform a computation and just ignore the result if it isn't needed.
Straightforward optimizations included tuning constants so that iterations decreased while the image quality is still acceptable. I set up initial conditions and coordinates to values that the Parent scheduler happened to work more efficiently with. I tightened up the state machine in the child module, coming up with a way to need only two states. I rewrote the scheduler so that it did not need a barrel-shifter. For the sum of two fixed-point products, I could right-shift the sum instead of the individual products. I was able to move most of the logic to assign statements.
I could save significant time by skipping computation inside the inner 'cardioid' shape. Because I rapidly learned that multipliers and multiplication were very expensive, I wondered if I could check if a pixel were in this cardoid shape without multiplying. Multiplication by a constant, though, I realized could be done very quickly. For example, multiplication by 320, as n320 == (n<<6) + (n<<8). Division by powers of 2, of course, I also converted into shifts.
I could also aggressively re-use computed values, such as how x^2 and y^2 could be used in both iteration and checking magnitude.
One attempt was to use an "approximation" abs(x)+abs(y) instead of the true magnitude, and to replace x^2-y^2 with (x+y)(x-y), saving one multiply. This changed the visual appearance in an unusual way:

I was pleasantly surprised to see in the logs that the Xilinx software could infer that the Child module was using a state machine, and could position the state reg in a more efficient way.
Implementation
I succeeded in synthesizing the project onto a Xilinx Spartan3 XC3s1500. To make the image look interesting, I shifted the color palette over time, making the colors move. The entire image is recomputed every time the colors shift, an intentional way of demonstrating how fast my system is. The results looked great, the redraw time was completely imperceptible.Working within the limitations of the specific hardware used, my final configuration was:
4 computing children
64 colors in palette
320x240 image
25Mhz clock speed
68,024 ticks to draw one frame at standard zoom
With a larger FPGA, I could have increased the number of children to drive these numbers higher. Even still, this math brought a smile to my face, remembering that each pixel requires several iterations:
68,024 ticks to compute 76,800 pixels
68,024 ticks @ 25Mhz to compute 76,800 pixels
0.00272096 seconds to compute 76,800 pixels
1 second to compute 28,225,332 pixels
Thanks to Prof. Mark Chang for access to equipment and a helpful discussion about state machines.
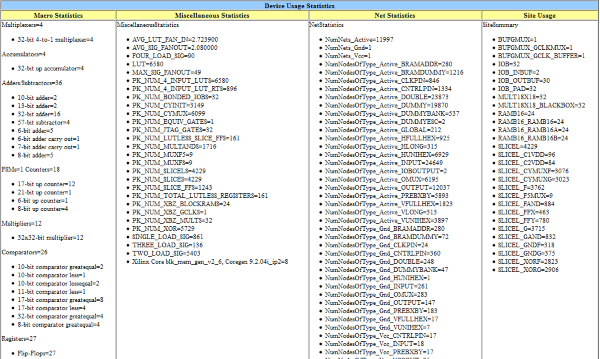
Device usage stats: