For an open-ended project in my Computer Science course, I wrote a program which will take a regular expression as an input, and generate a Nondeterministic Finite Automaton for recognizing that language. It can display this NFA graphically as well as generate Prolog code for simulating it and using it to match strings. In terms of practicality, this is the type of code that could be the basis for a regular-expression implementation used to build a tool like grep.
I use the symbol ',' to mean concatenation, and so where in grep you would enter 'abc' here you would enter 'a,b,c'. In the graphs, '.' refers to a null transition. Here are some sample inputs and outputs:
a,a*,b|c
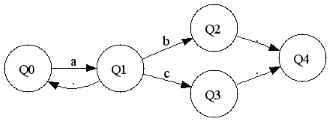(a|b),(a|b)*
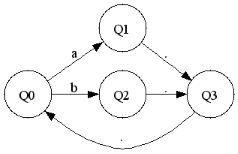(a|b),(a|b)
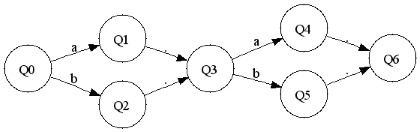In these examples '*', like in grep, repeats the group or more times. Disjunction uses the '|' symbol, for example 'a|b' means a or b. Unlimited levels of nested parenthesis are supported, thanks to recursion.
I process the expression recursively by at each point dividing the input string into two parts. The string '(a|b),b' is split into (a|b) and b with the operation ',' , and the first part is then split into a and b with the operation |. If the expression is a or a*, then it will return, and work its way down.
The Python program then will output Prolog code that can be consulted. The predicate parse can be used with a list to see if the string is recognized by the language.
Here is the Prolog code generated for (a|b),(a|b)
parse(L) :- start(S),
trans(S,L).
trans(X,[A|B]) :-
delta(X,A,Y),
write(X),
write(' '),
write([A|B]),
nl,
trans(Y,B).
trans(X,[A|B]) :-
nulltrans(X,Y),
trans(Y,[A|B]).
trans(X,[]):-
nulltrans(X,Y),
trans(Y,[]).
trans(X,[]) :-
final(X),
write(X),
write(' '),
write([]), nl.
delta(0,a,1).
delta(0,b,2).
delta(3,a,4).
delta(3,b,5).
nulltrans(1,3).
nulltrans(2,3).
nulltrans(4,6).
nulltrans(5,6).
nulltrans(99,99).
start(0).
final(6).| ?- parse([a,b]).
0 [a,b]
3 [b]
6 []
true ?
yes
| ?- parse([b,a]).
0 [b,a]
3 [a]
6 []
true ?
(15 ms) yes
| ?- parse([b,a,b]).
0 [b,a,b]
3 [a,b]
no